A capacitor is formed by two square metal-plates of edge a, separated by a distance d. Dielectrics of dielectric constants K1 and K2 are filled in the gap as shown in figure. Find the capacitance.

These two capacitors are connected in series.

To find out the capacitance, let us consider a small capacitor of
differential width dx at a distance x from
the left end of the capacitor.
The two capacitive elements of dielectric
constants K1 and K2 are with plate
separations as -
![]() and
and ![]() in series,
in series,
respectively as seen from fig.
Also, differential plate areas of the capacitors are adx.
We know, capacitance c is given by-
![]()
Where,
A= Plate Area
d= separation between the plates,
∈0 = Permittivity of free space = 8.854 × 10-12 m-3 kg-1 s4 A2
k = dielectric strengthof the material
Then, looking into the fig, the capacitances of the capacitive elements of the elemental capacitors are given by –
![]() and
and
![]()
We know that equivalent capacitance of capacitors connected in
series is given by the expression –
![]()
![]()
![]()
Now, integrating both sides to get the actual capacitance,
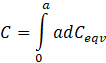
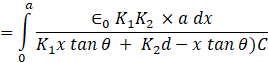
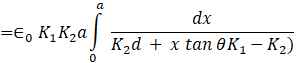
![]()
![]()
Looking back into the fig.
![]()
Substituting in the expression for capacitance C,
Now,

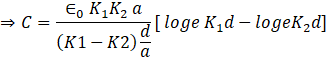
![]()