Consider an assembly of three conducting concentric spherical shells of radii a, b and c as shown in figure. Find the capacitance of the assembly between the points A and B.
These three metallic hollow spheres form two spherical capacitors, which are connected in series.

Solving them individually, for 1) and 2)
For a spherical capacitor formed by two spheres of radii ro > ri is given by
C =![]()
Where,
C: Capacitance
ri: inner radius
ro: outer radius
k: relative permittivity or dielectric constant
∈: permittivity of space
Similarly,
![]()
And
![]()
![]()
Now, the capacitors are connected in series, net capacitance for series connected capacitors is given by –
![]()
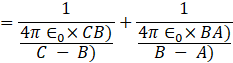

![]()
1