A parallel-plate capacitor having plate-area A and plate separation

d is joined to a battery of emf ϵ and internal resistance R at t = 0.


Consider a plane surface of area A/2, parallel to the plates and


situated symmetrically between them. Find the displacement current


through this surface as a function of time.



Given: Area of capacitor plates=A


Separation between the plates=d


Emf of the battery = ϵ


Internal resistance of the battery = R


Area of plane surface= A/2


Displacement current is the current which is generated by a time


varying electric field, not by the flow of charge carriers.


This current is also responsible for the generation of a time varying


magnetic field. The displacement current Id is generated due to the


fact that the charge on capacitor plates is changing with time.


The displacement current is given by



where ϕE is the time varying electric flux through the plane surface


and ϵ0 is the electric permittivity of free space(vacuum) and is equal


to 8.85 × 10-12 C2 N-1 m-2.


The electric field in the space between the plates can be given by


Guass’s Law. If the charge on the capacitor plate is Q and the area


of the plate is A(given), then by Guass’s law,



where E is the electric field and ϵ0 is the electric permittivity of free


space and dS is a small area element on the plate.


Further (because the area vector


and electric field lines are both normal to the surface and in


same direction i.e. θ=0° so cos θ=1)


So → , the electric field between the plates is .


This electric field produces and electric flux through the plane


surface given by



(because the area vector and electric field lines are both normal to


the surface and in same direction i.e. θ=0° so cos θ=1)



Now the charge on the capacitor is changing with time as it is


charging. If the capacitance of the capacitor is C, then the charge Q


at time t will be


where ϵ is the potential between plates which is equal to the emf of battery and R is the resistance attached in series.


The displacement current Id is given as






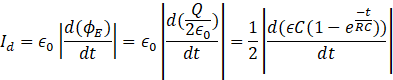
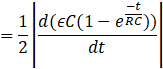
Thus the displacement current as a function of time is .


1
1