Consider the situation of the previous problem. Define displacement resistance Rd = V/id of the space between the plates where V is the potential difference between the plates and id is the displacement current. Show that Rd varies with time as
Rd = R (et/τ – 1)
Given: The displacement resistance ![]()
We will first calculate the displacement current.
The displacement current Id is generated due to the fact that the
charge on capacitor plates is changing with time.
The displacement current is given by
![]()
where ϕE is the time varying electric flux through the plane surface
and ϵ0 is the electric permittivity of free space(vacuum) and is equal
to 8.85 × 10-12 C2 N-1 m-2.
We need to calculate the electric flux through the capacitor plate.
As the charge on the capacitor plate at time t can be taken as Q so
by using Gauss’s law, we will calculate the electric flux.
According to Gauss’s law
![]()
so the electric flux would be
![]() .
.
As the capacitor is charging, the charge will be a function of time
given as
![]()
where C is the capacitance of the capacitor, V is the potential drop
at time t, R is the series resistance and V0 is the potential at time
t=0. Now the flux is ![]() .
.
Now by our definition, the displacement current is given by
![]()
which is
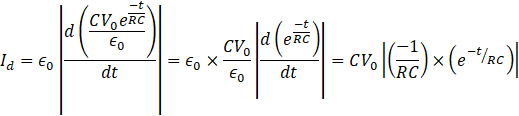
![]()
The displacement current is ![]()
We know that ![]()

therefore ![]() , where τ is the time constant.
, where τ is the time constant.