An ideal gas (C P /C V = γ) is taken through a process in which the pressure and the volume vary as p = αV b . Find the value of b for which the specific heat capacity in the process is zero.

Question

Philoid · Accepted Answer

Given:

p = aV^b

p = pressure, V = volume, a and b are constants.

Formula used:

We know, Q = U + ഽpdV from first law of thermodynamics,

where Q = change in heat, U = change in internal energy and ഽpdV = W = total work done, p = pressure, V = volume.

Since Q = nCdT, and U = nC_vdT, we get

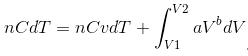… (ii), n = no. of moles, C = specific

heat capacity, and C_v = specific heat capacity at constant volume,

dT = change in temperature,

Since specific heat capacity is 0(given),

…(iii)

(after integration of 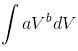from V₁ to V₂)

Now, from equation of state, PV = nRT,

Where

P = pressure,

V = volume,

n = number of moles,

R = universal gas constant,

T = temperature.

Substituting p = aV^b from (i):

aV^b+1 = nRT

=> … (iv)

Substituting (iv) in (iii),

(Since (T₂ - T₁) = dT)

=>

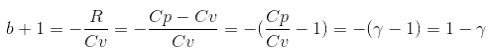
=> b = -

An ideal gas (CP/CV = γ) is taken through a process in which the pressure and the volume vary as p = αVb. Find the value of b for which the specific heat capacity in the process is zero.

An ideal gas (C_P/C_V = γ) is taken through a process in which the pressure and the volume vary as p = αV^b. Find the value of b for which the specific heat capacity in the process is zero.