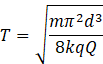Repeat the previous problem if the particle is displaced through a distance x along the line AB.
Given:
Charge of particles A and B : q = Q
Separation between A and B : d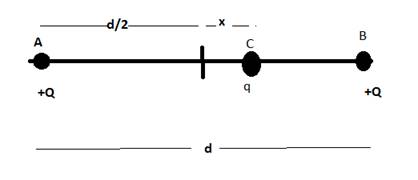
Here x is the displacement of particle C along AB.
Distance between A and C is : 
Distance between B and C is : 
Formula used:
For part (a), we will be using Coulomb’s Law,
Where F is the electrostatic force on B due to A, k is a constant .
k = 
= 9× 109 Nm2C-2 and r is the distance between the two charges.
q1=q2=Q.
now, the net force acting on C is:
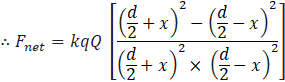
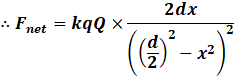Fnet is the net electric force experience by particle C of charge q.
(b)
When x≪d,
x2≪(d/2)2
Thus x2 can be neglected.
We get,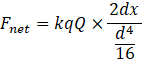
∴ Fnet α x
Thus, when x≪d force is proportional to x
(c)
The condition for Simple harmonic Motion of a particle is:
F'=mω2x
Here, m is the mass of the particle C, ω is the angular frequency.
Let Fnet = F’
Thus comparing two equations of F’, we get
We know that 
Where t is the Time Period.
Hence time period when particle is displaced along AB is
