Positive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x <<R, find the time period of oscillation of the particle if it is released from there.
Given:
Charge on the ring: Q
Radius of the ring : R
Charge of the particle at point P : q
Mass of the particle : m
Distance of P from the centre of the ring: x
Distance of P from the element A : l
Formula used:
Electric force is given as:
Where F is the electric force, q is the charge and E is the electric field.
Newton’s Law gives : 
Time period is given as: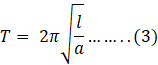
Where, l is the length. In this case OP=x and a is the acceleration.
Where F is the electric force, q is the charge and E is the electric field.
Consider an element of charge dQ on the ring at A.
Electric field at P due to the element A is given as:
Here, dE is the electric field due to element A. k= 
=9× 109 Nm2C-2, dQ is the charge of the element A and l is the distance between A and P.
Now,
And
Ecosθ
Therefore, the net electric field at P due to the entire ring is:
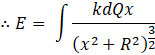
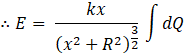
Therefore substituting in equation (1) we get,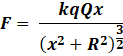
Here, F is the electric force on the particle due to entire charged ring.
Now the condition given in the question is x≪R. Thus, x2 can be neglected.
Hence using equation (2) and (3) we get,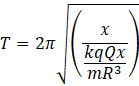
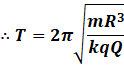Putting the value of k: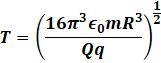
Hence time period of oscillation of the particle is 