A circular wire-loop of radius a carries a total charge Q distributed uniformly over its length. A small length dL of the wire is cut off. Find the electric field at the center due to the remaining wire.

Question

A circular wire-loop of radius a carries a total charge Q distributed uniformly over its length. A small length dL of the wire is cut off. Find the electric field at the center due to the remaining wire.

Philoid · Accepted Answer

Given:
Radius of the circular loop : a
Total charge on the wire : Q
Length of the cut off wire: dL
Formula used:
Electric field is given as:
Here, k is a constant and k= =9× 10⁹ Nm²C^-2 . q is the point charge and r is the distance between the charge and the point of influence.
Here r=a=radius of the loop.

We know that, electric field at the center of the uniformly charged circular wire

Which means that sum of electric field due to cut off wire and remaining wire is zero.
We know that,
Where λ is the linear charge density. Q is the total charge and L is the length of the wire.
Charge on the element dL be dq:

Here L = 2πa=circumference. Here, a is the radius of the loop and L is the Length of the loop.

Thus, electric field due to dL(cutoff wire) at the center is:

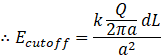
Since

Thus, magnitude of electric field at the center of the circular wire due to remaining wire is E= but in opposite direction to that of the field due to cut off wire.