A ball of mass 100g and having a charge of 4.9 × 10–5 C is released from rest in a region where a horizontal electric field of 2.0 × 104 C NC–1 exists.
(a) Find the resultant force acing on the ball.
(b) What will be the path of the ball?
(c) Where will the ball be at the end of 2s?
Given:
Mass of the ball : m = 100 g = 100× 10-3 kg =0.1 kg
Charge on the ball : q = 4.9 × 10–5 C
Horizontal electric field : E= 2.0 × 104 C NC–1
Initial Velocity of the ball: u = 0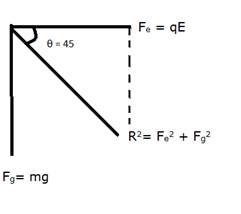
Here, R is the resultant Force due to gravitational force Fg and electric force Fe.
Formula used:
(a)
Electric force Fe due to charge q and electric field E is
Fe = qE
Gravitational force Fg experience due to mass of the ball m and acceleration due to gravity g is:
Fg=mg
Thus we see that Fe = Fg
The Resultant force R can be calculated by:
R2=Fe2+Fg2
∴ R2= (0.98)2+(0.98)2
∴R=√1.9208
∴R=1.3859 N
Hence the resultant force of 1.3859 N is acting on the ball.
(b)
We take tangent of the angle θ
But Fg= Fe,
Hence, the path of the ball is along a straight line and inclined at an angle of 45° with the horizontal electric field.
(c)
Here, we will be using one of the equations of motion.
Here s is the distance covered by the ball, u is the initial velocity of the ball, a is the acceleration of the ball and t is the time required to cover s.
We need to find s at t=2s
Firstly ,vertical displacement due to gravitational force is:a=g
Secondly,
Horizontal displacement due to electric force is:
Thus net displacement = (sv2+ sh2)1/2
∴ Net displacement = ((19.6)2+(19.62))1/2
∴ Net displacement = 27.71 m
Thus, the ball will be at a distance of 27.71m after 2s