The base of an equilateral triangle with side 2a lies along the y-axis such that the mid-point of the base is at the origin. Find the vertices of the triangle.

Key points to solve the problem:

• Idea of distance formula- Distance between two points P(x₁,y₁) and Q(x₂,y₂) is given by- PQ =

• Equilateral triangle- triangle with all 3 sides equal.

• Coordinates of midpoint of a line segment – Let P(x₁,y₁) and Q(x_2,y₂) be the end points of line segment PQ. Then coordinated of midpoint of PQ is given by –

Given, an equilateral triangle with base along y axis and midpoint at (0,0)

∴ coordinates of triangle will be A(0,y₁) B(0,y₂) and C(x,0)

As midpoint is at origin ⇒ y₁+y₂ = 0 ⇒ y₁ = -y₂ …..eqn 1

Also length of each side = 2a (given)

∴ AB = ….eqn 2

∴ from eqn 1 and 2:

y₁ = a and y₂ = -a

∴ 2 coordinates are – A(0,a) and B(0,-a)

See the figure:

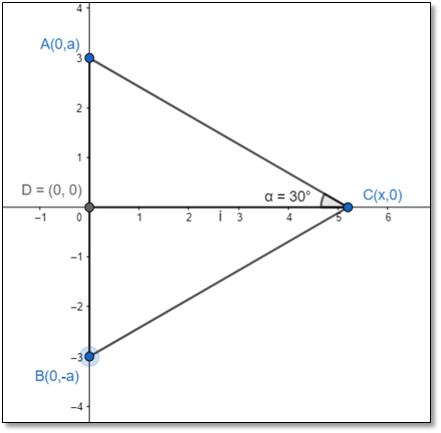
Clearly from figure:

DC = x

Also in ΔADC: cos 30° =

∴

Squaring both sides:

∴

∴ Coordinates of C are (√3a,0) or (-√3a,0)