A rod of length l slides between the two perpendicular lines. Find the locus of the point on the rod which divides it in the ratio 1 : 2.

Key points to solve the problem:

• Idea of distance formula- Distance between two points A(x₁,y₁) and B(x₂,y₂) is given by- AB =

• Idea of section formula- Let two points A(x₁,y₁) and B(x₂,y₂) forms a line segment. If a point C(x,y) divides line segment AB in ratio of m:n internally, then coordinates of C is given as:

C =

How to approach: To find locus of a point we first assume the coordinate of point to be (h, k) and write a mathematical equation as per the conditions mentioned in question and finally replace (h, k) with (x, y) to get the locus of point.

Let the coordinates of point whose locus is to be determined be (h, k). Name the moving point be C

Assume the two perpendicular lines on which rod slides are x and y axis respectively.

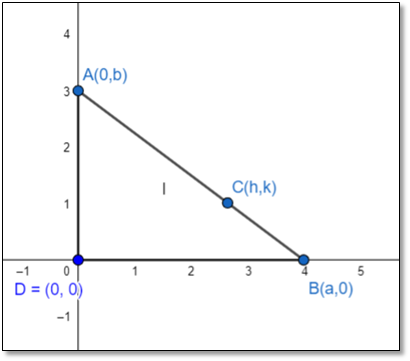
Here line segment AB represents the rod of length l also ΔADB formed is a right triangle. Coordinates of A and B are assumed to be (0,b) and (a,0) respectively.

∴ a² + b² = l² …eqn 1

As, (h,k) divides AB in ratio of 1:2

∴ from section formula we have coordinate of point C as-

C = =

As, a and b are assumed parameters so we have to remove it.

∵ h = 2a/3 ⇒ a = 3h/2

And k = b/3 ⇒ b = 3k

From eqn 1:

a² + b² = l²

∴

⇒

Replace (h,k) with (x,y)

Thus, locus of point on rod is: