If f is defined by f (x) = x2 – 4x + 7, show that 
We are given with a polynomial function f(x) = x2 - 4x + 7, and we have to f ‘(x) it’s value at
x = 5 and x = 
, so by using the formula, f ‘(c) = 
, we get,
f ‘(5) = 
f ‘(5) = 
f ‘(5) = 
f ‘(5) = 
f ‘(5) = limx→5 (x + 1) = 6
Hence to function is differentiable at x = 5 and has value 6 .
f ‘(
) = 
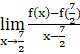
f ‘(
) = 
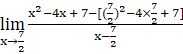
f ‘(
) = 
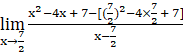
f ‘(
) = 
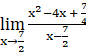
f ‘(
) = 
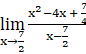
f ‘(
) = 
f ‘(
) = 
= 3
Therefore f ‘(5) = 2f ‘(
) = 6,
Hence, proved.
1