Discuss the continuity and differentiability of f (x) = e |x|.
We have to find the differentiability and the continuity of the function which we will do by considering both graphical and algebraic methods.
Now f(x) = e│x│, as we know that log x function is continuous in its domain and hence it is also derivable, but after we introduce modulus function, there might be the formation of sharp corners as the graph’s direction changes to its mirror reflection.
The graph of the function is,
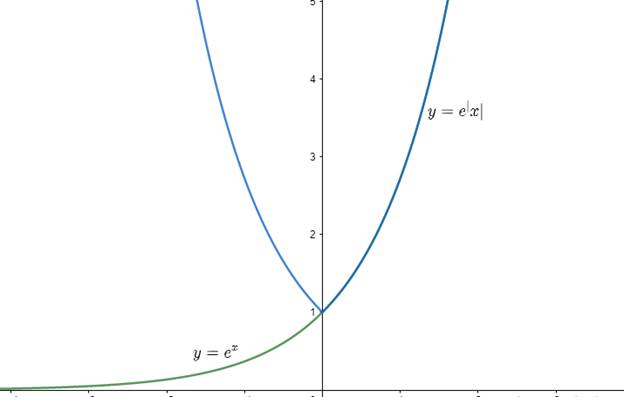
As we know that,
f(x) = e│x│, so by opening the modulus function by limiting the domain we get,
f(x) = {
We can put equality to any one of the two sub-functions.
Now we need to find the continuity around the point x = 0 because it is the common point between the two sub-functions, now the condition for the continuity to be there-there must be the satisfaction of the one condition which is,
L.H.L = R.H.L = f(x = c)
Which can further be elaborated as, at x = c
= f(c) = finite quantity,
L.H.L. = 
Put x = 0 - h
= 
= 1
R.H.L. = 
Put x = 0 + h
= 
= 1
f(x = 0) = ex = e - x = 1
Hence the function is a continuous function because it satisfies the required condition of continuity.
Now we have to check the function for derivability.
For which the condition is,
L.H.D. = R.H.D. = finite quantity.
The rule for derivability.
So by using the formula,
f ‘(c) = 
, we get,
f ‘(0 - ) = 
f ‘(0 - ) = 
put x = 0 - h,
f ‘(0 - ) = 
= - 1
This above is for the L.H.D.
Now we are doing for the R.H.D.,
f ‘(0 + ) = 
put x = 0 + h,
f ‘(0 + ) = 
= 1
As we can see that L.H.D. ≠ R.H.D.,
Hence we will say that this function is not derivable but it is continuous.