The gravitational force between a hollow spherical shell (of radius R and uniform density) and a point mass is F. Show the nature of F vs r graph where r is the distance of the point from the centre of the hollow spherical shell of uniform density.

Given:

Radius of hollow shell = R

Distance of point mass from centre of hollow shell = r

Let the mass of the spherical shell be M and the point mass be m. Then the force between the shell and the point mass is given by,

When point mass is positioned such that it is inside the hollow sphere i.e. 0<r<R, the force is zero as the mass of the hollow sphere is distributed on its surface. When the mass is positioned such that r≤R, the force will be,

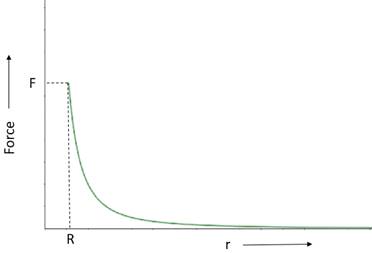
Therefore, the graph will be as follows