In the given figure, DEFG is a square and ∠BAC = 90⁰. Show that FG²= BG x FC.

OR

In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.

Given - DEFG is a square and ∠BAC = 90⁰

To prove - FG²= BG x FC

Property – If one triangle is similar to the second triangle and the second triangle is similar to the third triangle then the first triangle is similar to the third one.

Answer –

DEFG is a square, therefore we can write,

DE = EF = FG = GD ………(1) (sides of a square)

As opposite sides of square are parallel.

∴ DE || FG

∴ ∠ADE = ∠DBG ………(2) (corresponding angles)

∴ ∠AED = ∠ECF ………(3) (corresponding angles)

As given, ∠BAC = 90⁰

Now, in ∆ADE & ∆GBD,

∠DAE = ∠DGB ………angles of 90⁰

∠ADE = ∠DBG ………from (2)

………by AA test of similarity

Now, in ∆ADE & ∆FEC,

∠DAE = ∠EFC ………angles of 90⁰

∠AED = ∠ECF ………from (3)

………by AA test of similarity

By property, if one triangle is similar to the second triangle and the second triangle is similar to the third triangle then the first triangle is similar to the third one.

As and

………corresponding sides of similar triangles

∴ GD × EF = BG × FC

∴ FG × FG = BG × FC ………from (1)

∴ FG² = BG × FC

Hence proved !!!

OR

Consider an equilateral triangle ABC with altitude CD drawn on side AB.

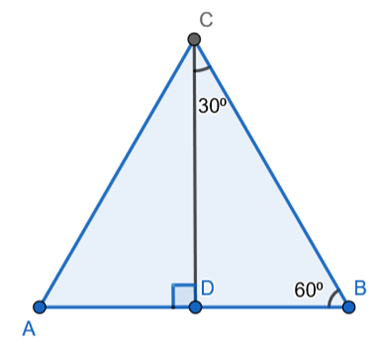
Given - ∆ABC is an equilateral triangle and CD is altitude drawn on side AB

To Prove – 3 BC² = 4 CD²

Property – Measure of all angles of an equilateral triangle are of 60⁰.

Answer –

As CD ⊥ AB.

∴ ∠BDC = 90⁰ ……….(1)

As measure of all angles of an equilateral triangle are of 60⁰.

∴ ∠CBD = 60⁰ ……….(2)

As sum of all angles of a triangle is 180⁰

∴ for ∆BCD,

∠BDC + ∠CBD + ∠DCB = 180⁰

∴ 90⁰ + 60⁰ + ∠DCB = 180⁰

∴ 150⁰ + ∠DCB = 180⁰

∴ ∠DCB = 30⁰

Therefore, ∆BCD is a 30⁰-60⁰-90⁰.

Now, in ∆BCD,

Squaring on both sides,

∴ 3 AB² = 4 AD²

Thus, three times the square of one side is equal to four times the square of one of its altitudes.

Hence proved !!!