Draw a triangle ABC with side BC = 6.5 cm, ∠B = 30⁰, ∠A = 105⁰. Then construct another triangle whose sides are times the corresponding sides of the triangle ABC.
OR

Construct a pair of tangents to a circle of radius 3 cm which are inclined to each other at an angle of 60°.

Question

Philoid · Accepted Answer

1. Construction of ∆ABC

We know that, sum of angles of triangle is 180⁰.

∴ ∠A + ∠B + ∠C = 180⁰

∴ 105⁰+ 30⁰ + ∠C = 180⁰

∴ 135⁰ + ∠C = 180⁰

∴ ∠C = 45⁰

Step 1 : Draw seg BC of length 6.5 cm

Step 2 : Draw a vector CC’ at an angle of 45⁰ at C.

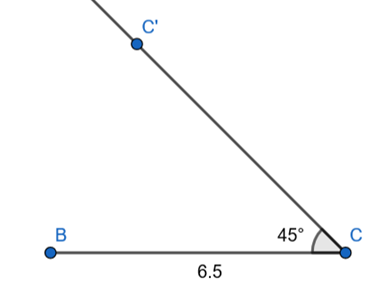
Step 3 : Draw a vector BB’ at an angle of 30⁰ at B.

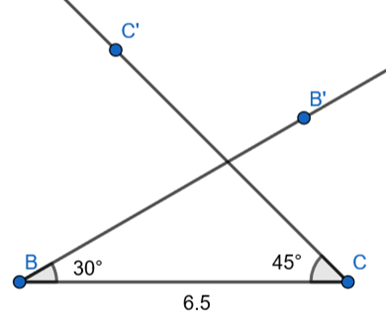
Step 4 : Take point of intersection of BB’ and CC’ and label it as A.

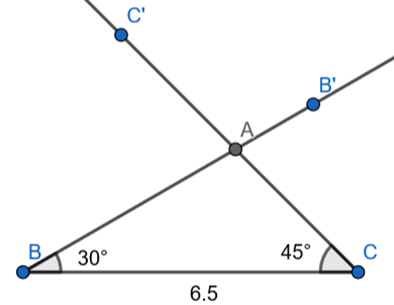
2. Construction of ∆PQR ∆ABC

As sides of ∆PQR are times corresponding sides of ∆ABC.

Angles of similar triangles are equal.

∴ ∠Q = 30⁰

∴ ∠R = 45⁰

Step 1 : Draw seg QR of length 4.875 cm

Step 2 : Draw a vector RR’ at an angle of 45⁰ at R.

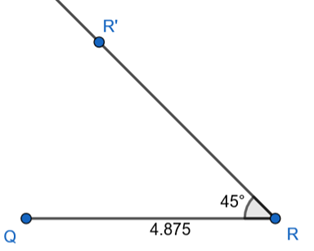
Step 3 : Draw a vector QQ’ at an angle of 30⁰ at Q.

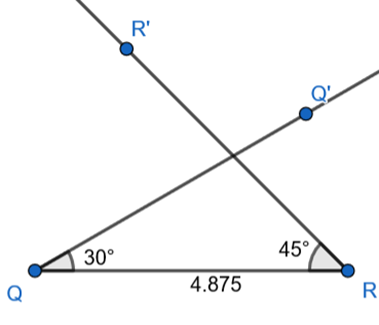
Step 4 : Take point of intersection of QQ’ and RR’ and label it as P.

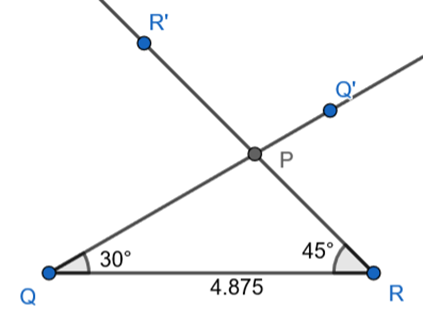
OR

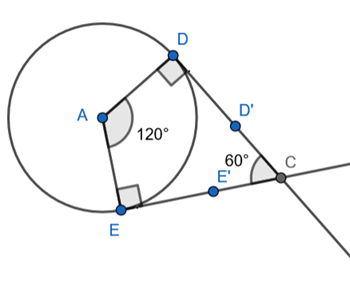
Let us draw a rough figure,

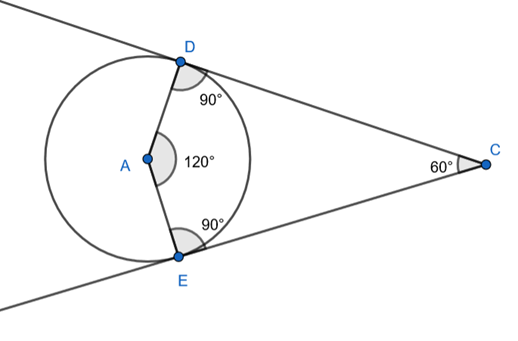
We know that, tangent is perpendicular to the radius at the point of contact.

∴ ∠D = ∠E = 90⁰

Angle between two tangents is 60⁰

∴ ∠C = 60⁰

Sum of all angles of a quadrilateral is 360⁰.

Therefore, for quadrilateral ADCE,

∴ ∠A + ∠E + ∠C + ∠D = 360⁰

∴ ∠A + 90⁰ + 60⁰ + 90⁰ = 360⁰

∴ ∠A + 240⁰ = 360⁰

∴ ∠A = 120⁰

Construction –

Step 1 : Draw circle with centre A and radius 3 cm.

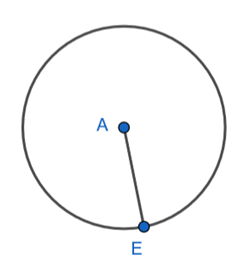
Step 2 : Draw radius AE.

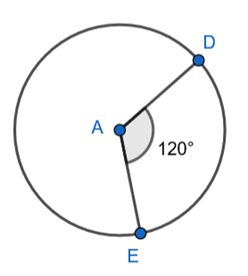
Step 3 : Draw radius AD at an angle of 120⁰ from radius AE.

Step 4 : Draw vectors EE’ and DD’ at an angle of 90⁰ from respective radii.

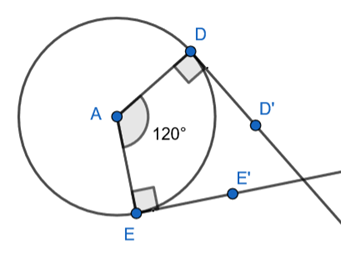
Step 5 : Take point of intersection of DD’ and EE’ and label it as C.

Draw a triangle ABC with side BC = 6.5 cm, ∠B = 30⁰, ∠A = 105⁰. Then construct another triangle whose sides are times the corresponding sides of the triangle ABC.ORConstruct a pair of tangents to a circle of radius 3 cm which are inclined to each other at an angle of 60°.