Consider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance R uniformly distributed along its length. The rod OA is made of rotate with a uniform angular speed ω as shown in the figure. Find the current in the rod when ∠AOC = 90°.

Question

Consider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance R uniformly distributed along its length. The rod OA is made of rotate with a uniform angular speed ω as shown in the figure. Find the current in the rod when ∠AOC = 90°.

Philoid · Accepted Answer

Given:

Resistance of circular loop = R

∠AOC = 90°

Angular velocity = w

Formula used:

From the previous problem, emf … (i), where B = magnetic field, w = angular velocity, a = radius

Now, since ∠AOC = 90°, the major and minor segments of the arc AC consist of parallel combination of resistances of R/4 and 3R/4 respectively (since the resistance is divided in the ratio of the angle at the centre).

Hence, equivalent resistance =

Therefore, current through the rod , where E = emf, R’ = equivalent resistance

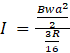⇒ = (Ans)