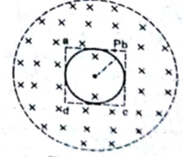
A uniform magnetic field B exists in a cylindrical region, shown dotted in figure. The magnetic field increases at a constant rate dB/dt. Consider a circle of radius r coaxial with the cylindrical region.

(a) Find the magnitude of the electric field E at a point on the circumference of the circle.

(b) Consider a point P on the side of the square circumscribing the circle. Show that the component of the induced electric field at P along ba is the same as the magnitude forum in part (a).

Given:

Magnetic field = B

Rate of increase of magnetic field = dB/dt

Radius = r

Formula used:

(a) Induced emf … (i), where = magnetic flux, t = time

Now, = B.A where B = magnetic field, A = area

Hence, … (ii)

For the circular loop, … (iii), where A = area, r = radius

Let the electric field be E

Hence, … (iv) ,where dr = element of length, E’ = emf

Hence, for this loop, , where r = radius

⇒

⇒ (Ans)

(b) When the square is considered, A = (2r)² = 4r², where A = area, r = radius

In this case, (perimeter of square)

Hence, from , where E = electric field, dr = length element, E’ = emf, we get

=> electric field (Ans)