Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between these points.

Question

Philoid · Accepted Answer

Given: Height of tower, CD = 15 m

Angle of depression of A from the top of tower, ∠DAC = 60°

Angle of depression of B from the top of tower, ∠DBC = 45°

To find: distance between two points A and B

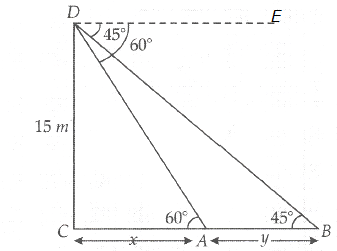
Lines DE & BC are parallel and DB is the transversal

∠EDB = ∠DBC [Alternate angles]

So, ∠DBC = 45°

Lines DE & BC are parallel and DB is the transversal

∠EDA = ∠DAC [Alternate angles]

So, ∠DAC = 60°

In right Δ DCA, we have

Rationalising

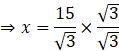
⇒ x = 5√3 …(i)

In right Δ DCB, we have

[from (i)]

⇒ 5√3 + y = 15

⇒ y = 15 – 5√3

⇒ y = 5(3 – √3)

∴ Distance between two points = 5(3 – √3)m