Draw a pair of tangents to a circle of radius 3 cm, which are inclined to each other at an angle of 60°.
OR

Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are 3/5 times the corresponding sides of the given triangle.

Question

Philoid · Accepted Answer

Step 1 : Draw a circle with radius 3 cm and centre O.

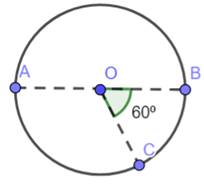
Step 2 : Draw any diameter AOB and Draw a radius OC such

such that BOC = 60°.

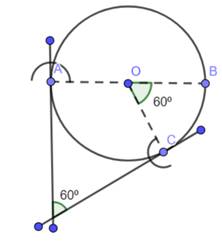
Step 3 : At C draw a perpendicular with OC and at A also

draw a perpendicular with OA.

OR

First we draw a right angle triangle

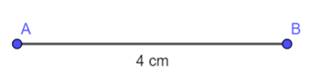
Step 1 : Draw a side AB of 4 cm with the help of scale.

Step 2 : Draw an perpendicular at point A with the help of compass. And cut 3 cm on it and named it as C.

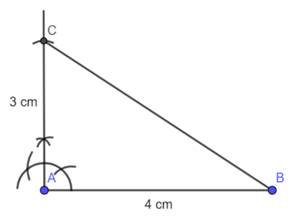
Now we draw a triangle similar to right triangle whose sides are 3/5 times the corresponding sides.

Step 1 : Draw a line from point A below the AB.

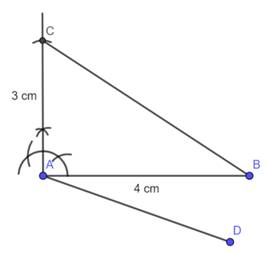
Step 2 : Cut the line AD in 5 equal parts from point A and name them A₁, A₂, A₃, A₄, A₅

Step 3 : Meet the point A₅ with B and make parallel to A₅B from A₃.

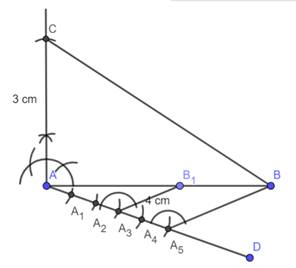
Step 4 : Make a line parallel to BC from B₁.

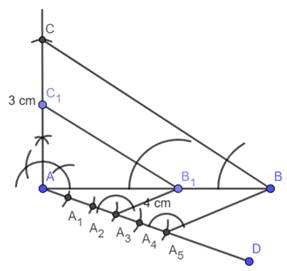
So, ∆ AB₁C₁ the required triangle whose corresponding side

is 3/5 of the right angle triangle.