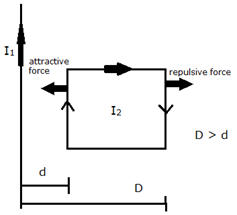
Consider the situation shown in figure. The straight wire is fixed but the loop can move under magnetic force. The loop will

The closest side of the loop to the straight wire carries a current in the same direction as the straight wire. So there will be an attractive force. And for the opposite side of the loop the current is moving in the opposite direction to that of the straight wire, so there will be a repulsive force. As the closest side shows attractive force and the farthest side shows repulsive force, the attractive force will be dominant. To explain it mathematically, we introduce the expression for force per unit length on each of the wires.
![]()
Where
F denote the force per unit length,
I1, I2 denote the currents in the two wires,
d is the distance between them
μ0 is the magnetic permeability of free space.
The current in the loop is of same magnitude everywhere. The parallel sides of the loop to the long straight wire will encounter all the force. As the side closer to the straight wire carries a current in the same direction, I1I2 will be positive thus it will encounter attractive force and the opposite side will encounter repulsive force as the, I1I2 is negative as the currents are in opposite directions. We can see that the force is inversely proportional to the distance. As the wire carrying current in the same direction is closer than the wire carrying current in the opposite direction, the attractive force will be greater than the repulsive force. The other two sides will experience forces of equal amplitude but opposite directions and thus will cancel each other out. Thus the loop will move towards the wire.