Figure shows a long wire bent at the middle to from a right angle. Show that the magnitudes of the magnetic fields at the points, P, Q, R and S are equal and find this magnitude.

Given:
Current through the wire : i
radius of the circle formed: d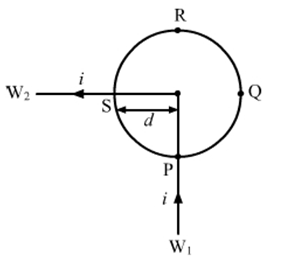

Let W₁ and W₂ be the terms for wire 1 and wire 2.
Arrow shows the direction of the current in the wire.
By right hand rule we can determine the direction of the magnetic field due to any of the two wire at any point.
Formula used:
By Ampere’s Law for a current carrying wire is
Here, B is the magnitude of magnetic field, μ₀ is the permeability of free space and μ₀= 4π × 10^-7 T mA^-1 and d is the distance between the current carrying wire and the required point. In this case, d is the radius of the circle.

(1) At point P,
Magnetic field at P due to W₁ is zero as P is on the axis of W₁.
Magnetic field at P due to W₂ is
Hence, net magnetic field at P due to both the wires is
Direction of B_P is perpendicular to the plane and in outward direction.
(2) At point Q,
Magnetic field at Q due to W₁,
Magnetic field at Q due to W₂ is zero as Q is not in the effective zone of W₂.
Hence, net magnetic field at Q due to both the wires is
Direction of B_Q is perpendicular to the plane and inward direction
(3) At point R,
Magnetic field at R due to W₁ is zero as R is not in the effective zone pf W₁.
Magnetic field at R due to W₂ is
Hence, net magnetic field at R due to both the wires is
Direction of B_R is perpendicular to the plane and in inward direction.
(4) At point S,
Magnetic field at S due to W₂ is zero as S is on the axis of W₂.
Magnetic field at S due to W₁ is
Hence, net magnetic field at S due to both the wires is
Direction of B_P is perpendicular to the plane and in outward direction.