A polygon of n equal sides is formed by bending a current carrying wire to total length 2πr which carries a current i.

(a) Find the magnetic field B at the center of the n-sided polygon.

(b) By letting n → ∞, derive the expression for the induced magnetic field at the center of a circular current carrying wire.

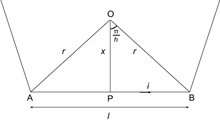
a) Using the diagram,

For a polygon of n equal sides, the angle at the centre is .

⇒

Considering angle to be very small

Using Biot–Savart’s law for one side of the n-sided polygon,

⇒

(substituting the value of r)

(substituting the value of l)

For n-sided polygon

B’ =nB

⇒

b) When n → ∞, polygon tends to a circle with radius r and magnetic field will tend toward