Find the speed at which the kinetic energy of a particle will differ by 1% from its nonrelativistic value 1/2 m₀v².

As we know that Kinetic energy gained by the electron is due to change in mass of electron.

As E=K.E=

As we know relativistic Energy is always more than non-relativistic kinetic energy because Rest energy is always less then apparent mass energy

The relativistic value of Kinetic energy will be

As we know the moving object appears to be heavier in the moving frame that’s because of Lorentz transformation known as apparent mass which is given by

Where , V is velocity of moving object and C is speed of light in vacuum i.e.

K.E=

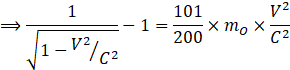
Let

As K= which is we can neglect