A parallel-plate capacitor has plate area 20 cm2, plate separation 1.0 mm and a dielectric slab of dielectric constant 5.0 filling up the space between the plates. This capacitor is joined to a battery of emf 6.0 V through a 100 kΩ resistor. Find the energy for the capacitor 8.9 μs after the connections are made.
Energy stored in a capacitor:
The energy stored in a capacitor with capacitance C , charge is given by:
where V is the potential difference across the capacitor.
Capacitance of a Capacitor in presence of a dielectric:
The capacitance of the capacitor is initially C0 and then a dielectric medium of dielectric constant K is inserted between the plates. The new capacitance is
Also for parallel plate capacitors,
Where ϵ0 is the permittivity of free space, A is the area of plate and l is the distance between the plates.
Charging a capacitor:
A capacitor of capacitance C is being charged using a battery of emf ϵ through a resistance R . A switch S is also connected in series with the capacitor. The switch is initially open. The capacitor is uncharged at first. At t=0, the switch is closed. The current through the circuit at anytime t>0 is given by:
Where I0 is the initial current.
The charge is given by:
Note that 
is known as time constant.
Given,
Area of the plate, 
(
Now, distance of separation: 
Dielectric constant, 
Emf of battery, 
Resistance ,
Time, 
Now,
Time constant, 
We want to find the charge on the capacitor at t = 8.9μs
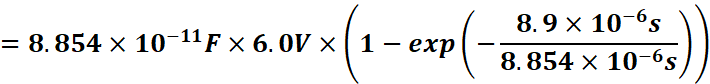
Now, energy of the capacitor is given by:
Hence, the capacitor stores 
of energy after 8.9μs.