Find the charge on each of the capacitors 0.20 ms after the switch S is closed in figure.

Question

Philoid · Accepted Answer

Concepts/Formulas used:

Charging a capacitor:

A capacitor of capacitance C is connected in series with a resistor of resistance R, a switch, and battery of emf ϵ . It is uncharged at first. The switch is closed at t = 0, then at time any time t the charge stored on the capacitor is given by

Capacitors in parallel:

If capacitors C₁, C₂, C₃ , … are in parallel, then the equivalent capacitance is given by:

If the charges on the capacitors are Q1, Q2, Q3, .. are in parallel, then the charge on the capacitor with equivalent capacitance is given by:

We can replace the two capacitors by another capacitor of capacitance C. As the capacitors are in parallel.

Now,

We know that

Here,

Also, and

Hence,

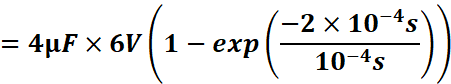
Let the charge on both the capacitors be Q. As both have the same capacitance and potential (, both must have the same charge. Note that they both are in parallel.

Hence,