A capacitor of capacitance C is given a charge Q. At t = 0, it is connected to an ideal battery of emf ϵ through a resistance R. Find the charge on the capacitor at time t.

Note that and .

Concepts/Formulas used:

Kirchhoff’s loop rule:

The sum of potential differences around a closed loop is zero.

Capacitance:

If two conductors have a potential difference V between the them and have charges Q and -Q respectively on them, then their capacitance is defined as

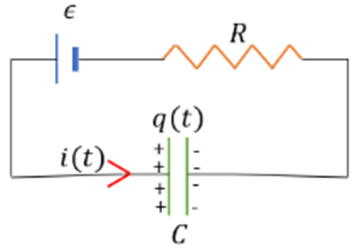
Let the potential across the capacitor be at time t be V_c. Let the charge at time t be q. The initial charge is Q.

Applying Kirchhoff’s loop rule ,

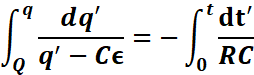
We know that

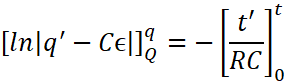
Using the property : , we get

Note that at any time,

Thus, we can remove the modulus,