A river is flowing from west to east at a speed of 5 meters per minute. A man on the south bank of the river, capable of swimming at 10 meters per minute in still water, wants to swim across the river in the shortest time. He should swim in a direction

Question

A river is flowing from west to east at a speed of 5 meters per minute. A man on the south bank of the river, capable of swimming at 10 meters per minute in still water, wants to swim across the river in the shortest time. He should swim in a direction

Philoid · Accepted Answer

Let us consider the width of the river be . Let the man swims at some angle with velocity . This is shown below in the figure

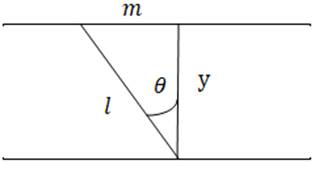
Where, =distance travelled by man and is constant

By Pythagoras theorem in above triangle formed, we have

Differentiating above equation with respect to time, we get

Negative sign is due to decrease in the distance, covered by man, as time goes. Man can also go along through the river with velocity .

Therefore, the equation (1) becomes

Therefore, time taken by the Man to pass the river with velocity along the line making angle is

Therefore, the man takes shortest time when is maximum. is maximum when . Thus, we say that the man should swim along that is towards north so that he crosses the river in shortest possible time.