Six particles situated at the corners of a regular hexagon of side a move at a constant speed u. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.

Question

Six particles situated at the corners of a regular hexagon of side a move at a constant speed u. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.

Philoid · Accepted Answer

A regular hexagon has a side= a.

Six particles situated at the corners of the hexagon are moving with a constant speed v.

As per the question, each particle maintains a direction towards the particle at the next corner.

So, particles will meet at centroid O of triangle PQR.

Now, at any instant, the particles will form an equilateral triangle PQR with the same centroid O.
We know that P approaches Q, Q approaches R and so on.

Now, we will consider the motion of particle P. Its velocity makes an angle of.
This component is the rate of decrease of distance PO.

Relative velocity between P and Q: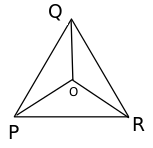

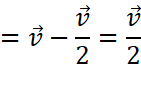
Hence, the time taken by the particles to meet each other is

.