An electron and a positron are released from (0, 0, 0) and (0, 0, 1.5R ) respectively, in a uniform magnetic field , each with an equal momentum of magnitude p = e BR. Under what conditions on the direction of momentum will the orbits be nonintersecting circles?

Question

An electron and a positron are released from (0, 0, 0) and (0, 0, 1.5R ) respectively, in a uniform magnetic field , each with an equal momentum of magnitude p = e BR. Under what conditions on the direction of momentum will the orbits be nonintersecting circles?

Philoid · Accepted Answer

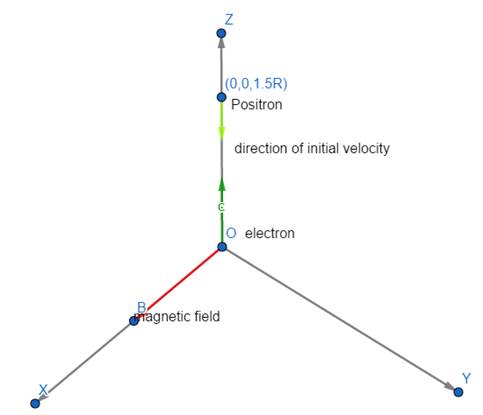
Because of electric charge the initial velocities are along –z for positron and +z for electron. Then it experiences Lorentz force and start rotation. The rotation is limited to the y-z plane as no involvement of any x directing components.

The momentum P is always perpendicular to the radius in circular motion.

Let us assume the momentum of the electron is P_electron and the positron is P_positron.

So, the coordinates of the center of their paths are going to be,

C_e = (0, Rsinθ, Rcosθ)

C_p = (0, -Rsinθ, 1.5R-Rcosθ)

The condition for the paths being non intersecting circles is that the distance between the centers is greater than 2R.

Distance between the center,

D² = (Rsinθ - (-Rsinθ)² + (Rcosθ - (1.5R – cosθ))²

= 4R²sin²θ + (2Rcosθ – 1.5R)²

= 4R²sin²θ + 4R²cos²θ – 6R²cosθ +2.25R ^{� � �} �²

= 6.25R² – 6R²cos²θ

From the condition; D²>4R²

6.25R² – 6R²cos²θ > 4R²

2.25/6 > cosθ

cosθ < 0.375