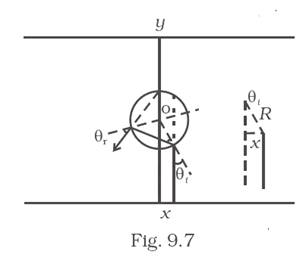
An infinitely long cylinder of radius R is made of an unusual exotic material with refractive index –1 (Fig. 9.7). The cylinder is placed between two planes whose normal are along the y direction. The center of the cylinder O lies along the y-axis. A narrow laser beam is directed along the y direction from the lower plate. The laser source is at a horizontal distance x from the diameter in the y direction. Find the range of x such that light emitted from the lower plane does not reach the upper plane.

Question

An infinitely long cylinder of radius R is made of an unusual exotic material with refractive index –1 (Fig. 9.7). The cylinder is placed between two planes whose normal are along the y direction. The center of the cylinder O lies along the y-axis. A narrow laser beam is directed along the y direction from the lower plate. The laser source is at a horizontal distance x from the diameter in the y direction. Find the range of x such that light emitted from the lower plane does not reach the upper plane.

Philoid · Accepted Answer

The range of x such that light emitted from the lower plane does not reach the upper plane

Given:

The radius of the cylinder = R, the refractive index of the cylinder = -1, placed in a y-axis coordinate with center at zero, the angle of incidence is and the angle of refraction is. The distance at which the cylinder is kept on y-axis is x.

Formula used:

Snell’s Law, is the ratio between the sine value of incidence and refraction with the ratio of refractive index of the mediums through which the light passes.

where

is the refractive index of the medium, is the refractive index of the air. i is the angle of incidence and r is the angle of refraction

Explanation:

The angle at which the rays will not reach the cylinder is from. The refracted ray coming out of the cylinder is. Therefore, the range for the angle of refraction in terms of angle of incidence is

Now the above range of x or where the cylinder should be kept to not get light on the plates is .