Consider the LCR circuit shown in Fig 7.6. Find the net current i and the phase of i. Show that 
. Find the impedance Z for this circuit.
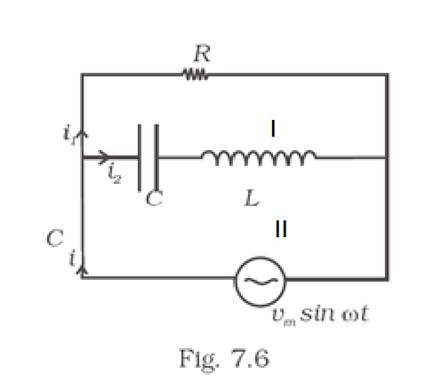
Given:
Current flowing through C and L : i2
Current flowing through R : i1
Supply AC voltage: v=vmsinωt
Formula used:
We know the equation for LCR circuit
Here, L is the inductance, di/dt is the rate of flow of current, R is the resistance, q is the charge, C is the capacitance and V is the AC voltage.
For first branch (I) consisting resistor R,
i1 is the current in the first branch and R is the resistance.
For the Second branch (II) consisting of Inductor and Capacitor,
Here, q2 is the charge due to current i2.
We know that, A.C value of charge is
qm is the maximum charge due to maximum current im and ϕ is the phase of the circuit. Substituting value of q2 we get.
If phase is zero then, ϕ =0
Thus current through branch 2: i2 = dq2/dt
As i1 and i2 have sin and cos terms respectively, we say that both are 90° out of phase. At ϕ =0
Also, total current would be: i=i1+i2
Let us use trigonometric property
Let
And
Here A = ((Acosϕ)2+(Asinϕ )2)1/2
Hence is the expression for total current.
Impedance is given as
V is the voltage and I is the current.
Hence is the expression for impedance of the given circuit.