In Fig. 4.236, and AP : PB = 1 : 2. Find [CBSE 2008]

Question

Philoid · Accepted Answer

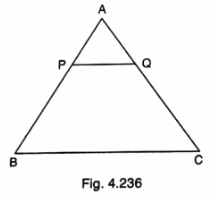
Given in the given figure PQ || BC and AP: PB = 1: 2

We know that basic proportionality theorem states that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.

Since Δ APQ and ΔABC are similar,

Given

⇒ PB = 2AP

So,

we know that the ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

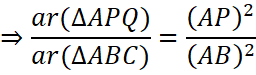
∴ Area (ΔAPB): Area (ΔABC) = 1: 9