![]() and
and ![]() are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangles ABC and BDE is
are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangles ABC and BDE is
Given ΔABC and ΔBDE are two equilateral triangles such that D is the midpoint of BC.

Since the given triangles are equilateral, they are similar triangles.
And also since D is the mid-point of BC, BD = DC.
We know that the ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
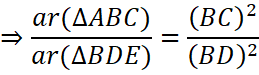

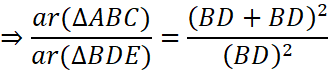

![]()
∴ ar (ΔABC): ar (ΔBDE) = 4: 1
1