In , a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects, then

A. BC =CY

B. BC = BY

C. BC CY

D. BC BY

Given in ΔABC, XY || BC and BY is a bisector of ∠XYC.

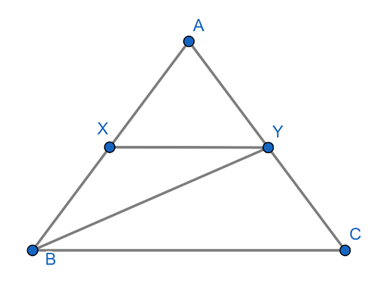
Since XY || BC,

∠YBC = ∠BYC [alternate angles]

Now, in Δ BYC, two angles are equal.

Hence, two corresponding sides will be equal.

∴ BC = CY