If ![]() is an equilateral triangle such that
is an equilateral triangle such that![]() , then AD2 =
, then AD2 =
Given in an equilateral ΔABC, AD ⊥ BC
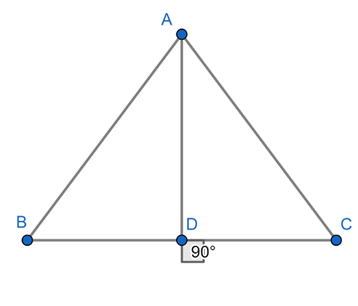
Since AD ⊥ BC, BD = CD = BC/2
We know that the Pythagoras theorem state that in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Now, in right triangle ADC,
⇒ AC2 = AD2 + DC2
⇒ BC2 = AD2 + DC2
⇒ (2DC)2 = AD2 + DC2
⇒ 4DC2 = AD2 + DC2
⇒ 3DC2 = AD2
∴ 3CD2 = AD2
1