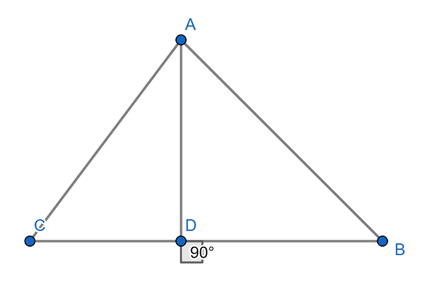
In a 
, perpendicular AD from A on BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then
Given in ΔABC, AD ⊥ BC, BD = 8 cm, DC = 2 cm and AD = 4 cm.
We know that the Pythagoras theorem state that in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Now, in right triangle ADC,
⇒ AC2 = AD2 + DC2
⇒ AC2 = (4)2 + (2)2
= 16 + 4
∴ AC2 = 20 … (1)
In ΔADB,
⇒ AB2 = AD2 + BD2 = 42 + 82 = 16 + 64
∴ AB2 = 80 … (2)
Now, in ΔABC,
⇒ BC2 = (CD + DB)2 = (2 + 8)2 = 102 = 100
And AB2 + CA2 = 80 + 20 = 100
∴ AB2 + CA2 = BC2
Hence, ΔABC is right angled at A.
1