is a right triangle right-angled at A and . Then, =

Given ΔABC is a right triangle right-angled at A and AD ⊥ BC.

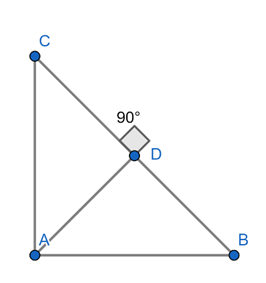
⇒ ∠CAD + ∠BAD = 90° … (1)

⇒ ∠BAD + ∠ABD = 90° … (2)

From (1) and (2),

∠CAD = ∠ABD

By AA similarity,

In ΔADB and ΔADC,

⇒ ∠ADB = ∠ADC [90° each]

⇒ ∠ABD = ∠CAD

∴ ΔADB ~ ΔADC

We know that if two triangles are similar, their corresponding angles are equal and corresponding sides are proportional.