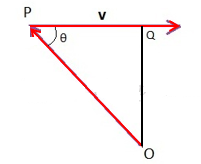
A particle moves on a given straight line with a constant speed υ. At a certain time, it is at a point P on its straight-line path. O is a fixed point. Show that is independent of the position P.

Question

Philoid · Accepted Answer

The velocity of the particle is . OP is the path followed by the particle.

x = k (k unit vector perpendicular to plain containing and v, and 180°-θ is the angle between them)

⇒ x = OP.v.sinθ k = v. (OP.sinθ) k =(v.) k

This expression is independent of θ or OP and constant because OQ is the perpendicular distance between line and point O. So x does not depend on the position P.