Consider a head-on collision between two particles of masses m₁ and m₂. The initial speeds of the particles are u₁ and u₂ in the same direction. The collision starts at t = 0 and the particles interact for a time interval ∆t. During the collision, the speed of the first particle vanes as

Find the speed of the second particle as a function of time during the collision.

Question

Philoid · Accepted Answer

Given that two particles of masses m₁ and m₂, has initial speed u₁ and u₂ respectively.

The collision starts at t = 0 and the particles interact for a time interval ∆t.

During the collision the speed of the two particles of masses m₁ and m₂ are u (t) and u’ respectively.

Now from law of conservation of momentum

Since,

Then,

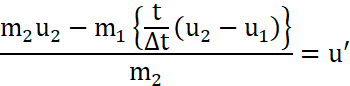
So, the speed of the second particle as a function of time during the collision will be