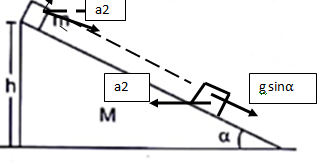
A block of mass m is placed on triangular block of mass M, which in turn is placed on a horizontal surface as shown in figure (9-E21). Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.



The block m will slide down the inclined plane of mass M with acceleration (relative to the inclined plane).


The horizontal component of a1 will befor which the block M will accelerate towards left.


Let the acceleration be a2. According to the concept of centre of mass, (in the horizontal direction) external force is zero.


123.PNG


Thus,




_________ (1)


So, the absolute acceleration of m on the block M alone the direction of the incline will be






________ (2)


Let the time taken by the block m to reach the bottom end be ‘t’


Now,





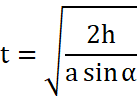
So, the velocity of the bigger block after time ‘t’ will be vm





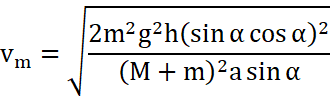
Now, putting the value of ‘a’ to the above equation




1
1