Suppose the rod with the balls A and B of the previous problem is clamped at the center in such a way that it can rotate freely about a horizontal axis through the clamp. The system is kept at rest in the horizontal position. A particle P of the same mass m is dropped from a height h on the ball B. The particle collides with B and sticks to it. (a) Find the angular momentum and the angular speed of the system just after the collision. (b) What should be the minimum value of h so that the system makes a full rotation after the collision.
Given:
Mass of particle P = m
Height from which it is dropped = h
Velocity of the particle P before collision with B= ![]()
Consider the bodies of particle P and ball B as a single system
Net external torque acting on the system is zero
![]()
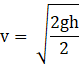
after the collision, the angular momentum of the rod
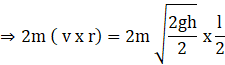
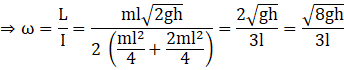
(B) When mass 2m is at top of the rod and mass m is at the bottom, the rod will rotate automatically. The total potential energy will be given as
![]()
Therefore,
![]()
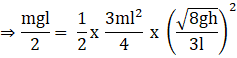
![]()