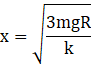Figure (8-E15) shows a smooth track, a part of which is a circle of radius R. A block of mass m is pushed against a spring of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal.

The distance covered is given as

Given

The spring constant is given as k, the mass of the block is given as m, and a slide with semi circle is given as well.

Formula Used

Using the conservation of static and dynamic energy such as centripetal and kinetic energy, we have the conservation equation as

where

m is the mass of the object, v is the velocity, k is the spring constant and x is the elongation distance, R is the radius of the circular part, r is the radius of the object.

Explanation

The energy of the block in form of kinetic energy is equated with the centripetal energy of the surface making the equation as

Taking the velocity of the block in terms of radius as, placing the velocity we have

Hence, the distance covered is