Consider an ice cube of edge 1.0 cm kept in a gravity-free hail. Find the surface
area of the water when the ice melts Neglect the difference in densities of ice and water.
(36 π)1/3 cm2
Given, volume is ![]()
As the densities are to be neglected, we assume that the volumes do not change when state changes.
As gravity has no effect here, the water after melting will form a sphere(least surface area) of radius ![]() .
.
Hence, ![]()
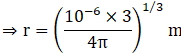
The surface area of the sphere will then be
![]()
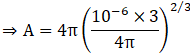

![]()
1