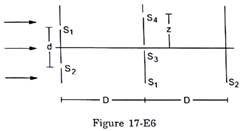
Consider the situation shown in figure (17-E6). The two slits S1 and S2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen ∑1 placed at a distance D from the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3. Another screen ∑2 is placed a further distance D away from ∑1. Find the ratio of the maximum to minimum intensity observed on ∑2 if z is equal to
(a) 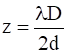
(b) 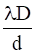
(c) 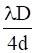
Let the intensity of slits ![]() and
and ![]() be
be ![]() . The amplitude through each slit be
. The amplitude through each slit be ![]() .
.
For ![]() , the phase difference is zero as it lies in the center of the screen. So here, the intensity(
, the phase difference is zero as it lies in the center of the screen. So here, the intensity(![]() ) would be maximum.
) would be maximum.
![]()
For ![]() , the path difference is
, the path difference is ![]()
And the corresponding phase difference is
![]()
(a) For ![]() ,
,
![]()
This is the condition of destructive interference, so the intensity at ![]() is zero. Hence, only one of the slits is illuminated and so the pattern on Σ₂ would be uniform with no maxima or minima. As maxima and minima are same, the ratio is one.
is zero. Hence, only one of the slits is illuminated and so the pattern on Σ₂ would be uniform with no maxima or minima. As maxima and minima are same, the ratio is one.
(b)For ![]() ,
,
![]()
In this case, constructive interference is taking place at ![]() . So the intensity is maximum and is equal to
. So the intensity is maximum and is equal to ![]() that is
that is ![]() .
.
In this case, slits ![]() and
and ![]() will form an interference pattern with alternate dark and bright fringes. Let the maximum intensity be
will form an interference pattern with alternate dark and bright fringes. Let the maximum intensity be ![]() while the minimum will be zero for a dark fringe.
while the minimum will be zero for a dark fringe.
Hence the ratio is ![]() .
.
(c)For ![]() ,
,
![]()
The intensity at ![]() is thus
is thus ![]() .
.
And intensity at ![]() is
is ![]()
Let the amplitude at ![]() be
be ![]() and at
and at ![]() be
be ![]() .
.
Therefore,
![]()
![]()
And
![]()
![]()
So maximum amplitude at Σ₂ would be ![]() and minimum amplitude would be
and minimum amplitude would be ![]() .
.
Hence, the ratio of intensities is
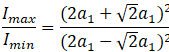

Rationalizing,
![]()