(a) Derive the expression for the potential energy of an electric dipole of dipole moment placed in a uniform electric field .
Find out the orientation of the dipole when it is in (i) stable equilibrium, (ii) unstable equilibrium.

(b) Figure shows a configuration of the charge array of two dipoles. Obtain the expression for the dependence of potential on r for r >> a for a point P on the axis of this array of charges.

OR

(a)Define electric flux. Write its S.I. unit.

(b)Using Gauss’s law, obtain the electric flux due to a point charge ‘q’ enclosed in a cube of side ‘a’.

(c)Show that the electric field due to a uniformly charged infinite plane sheet at any point distant x from it, is independent of x.

Question

(a) Derive the expression for the potential energy of an electric dipole of dipole moment placed in a uniform electric field .
Find out the orientation of the dipole when it is in (i) stable equilibrium, (ii) unstable equilibrium.

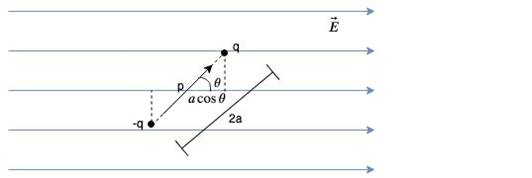
(b) Figure shows a configuration of the charge array of two dipoles. Obtain the expression for the dependence of potential on r for r >> a for a point P on the axis of this array of charges.

OR

(a)Define electric flux. Write its S.I. unit.

(b)Using Gauss’s law, obtain the electric flux due to a point charge ‘q’ enclosed in a cube of side ‘a’.

(c)Show that the electric field due to a uniformly charged infinite plane sheet at any point distant x from it, is independent of x.

Philoid · Accepted Answer

(a) The following figure shows an electric dipole with charges and separated by a distance in a electric field .

The dipole moment is given by

Now, the torque on the dipole is

Therefore, work done by this torque in rotating the dipole is

Now, let and

Now, for stable equilibrium,

And unstable equilibrium gives

(b) From the figure it is evident that the potential at point P is due to three charges.

Where potential is given by where , q is the charge and r is the distance of the point from the charge.

Now for

OR

(a) Electric flux is the amount of electric field crossing a given area or the integral of electric field over a given surface. Mathematically,

(b) The gauss law states that the total flux crossing a surface is directly proportional to the amount of electric charge held within the surface.

Here, the charge enclosed by the cube is q. Therefore, the flux is

(c) To calculate flux, we create a hypothetical Gaussian pill box through the surface. The area of the face of the cylinder is while the electric field is .

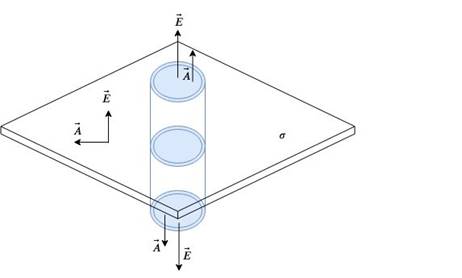
The area and the field are at right angles throughout the surface of the cylinders except the faces.

Hence in the curved surface area, the flux is

At either side, the flux is

Total flux thus becomes (due to the two surfaces)

So the electric field has no dependence on distance, and only depends on the charge density of the sheet.