(a) In Young’s double slit experiment, deduce the conditions for obtaining constructive and destructive interference fringes. Hence deduce the expression for the fringe width.
(b) Show that the fringe pattern on the screen is actually a superposition of single slit diffraction from each slit.
(c) What should be the width of each slit to obtain 10 maxima of the double slit pattern within the central maximum of the single slit pattern, for green light of wavelength 500 nm, if the separation between two slits is 1 mm ?
OR
(a) Two thin convex lenses L1 and L2 of focal lengths f1 and f2 respectively, are placed coaxially in contact. An object is placed at a point beyond the focus of lens L1. Draw a ray diagram to show the image formation by the combination and hence derive the expression for the focal length of the combined system.
(b) A ray PQ incident on the face AB of a prism ABC, as shown in the figure, emerges from the face AC such that AQ = AR. Draw the ray diagram showing the passage of the ray through the prism. If the angle of the prism is 60°and refractive index of the material of the prism is 3, determine the values of angle of incidence and angle of deviation.
(a) Young’s double slit experiment explains the phenomenon of interference of light. Let us consider two slits S1 and S2 that are small distance d apart. Let the source of light of wavelength is kept behind the slits. The screen GG′ is kept at a distance D from the slits.
The two waves coming out from slits S1 and S2 superimpose on each other and forms a pattern of interference.
Let O be the centre of the distance between the slits. The intensity of light at any point on screen will depend on the path difference between the two waves reaching that point.
Let us consider a point P which is at x distance from O on the screen. Path difference between two waves at P = S2P − S1P
The intensity at the point P is maximum if the path difference is an integral multiple of wavelength and minimum if it is odd integral multiple of half wavelength.
If the maxima is observed at point P then, we must have S2P − S1P = n, n = 0, 1, 2, 3...
From the given figure, we can write
![]()
On solving the above equation, we get
![]()
![]()
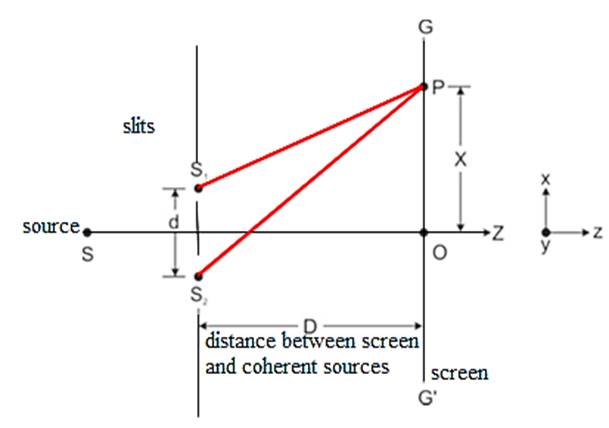
As d<<D, then S2P+S1P=2D
![]()
Hence path difference is given as ![]()
For constructive interference, the bright fringe is formed and the path difference will be written as ![]() , where n= 0,1,2,3,….
, where n= 0,1,2,3,….
![]()
For destructive interference, the dark fringe is formed and the path difference will be written as ![]() , where n= 0,1,2,3,….
, where n= 0,1,2,3,….
![]()
The fringes are equally spaced and the distance between them is given as
![]()
![]()
![]()
Therefore, the fringe width is given as ![]()
(b) In Young’s double slit experiment, the pattern observed is due to two phenomena. One is diffraction which occurs due to the single slit while another is interference which corresponds to double slit. When one of the slits say S1 is closed by any object and light is allowed to pass through one slit only, when the diffraction pattern will be observed on the screen. Similarly, the similar pattern will be observed if the slit S2 is closed and the other slit is exposed to light source. hence. We can say that the pattern observed in double slit experiment is the result of diffraction from each slit.
The actual double slit intensity pattern consists of the interference pattern (solid lines) formed within the diffraction pattern (dotted lines).
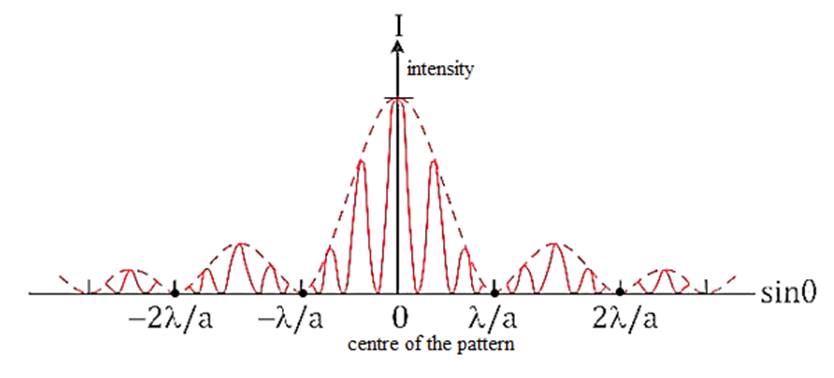
(c) Let the width of each slit = a
The separation between n maxima in a double slit experiment is given as
![]()
where D is the distance between the slit and screen, d is the separation between the two slits. The angular separation between n maxima is given as
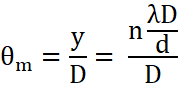
![]()
The angular separation between 10 bright fringes can be written as
![]()
The angular width of the central maximum in the diffraction pattern due to a single
slit of width ‘a’ is given by
![]()
It is given that 10 maxima of the double slit pattern is formed within the central
maximum of the single slit pattern.
Therefore, we can equate (1) and (2) as
![]()
![]()
The separation between the slits, d = 1 mm
Therefore, the slit width a = 1/5= 0.2mm
OR
(a) Consider there are two thin lens L1 and L2 of focal length f1 and f2 placed coaxially in contact with each other. Let P be the point where the optical centres of the lenses coincide (lenses being thin).
Let the object is at a point O beyond the focus of lens L1 such that OP = u (object distance). Lens L1 separately forms the image at I1 where PI1 = v1 (image distance).
The image I1 would serve as a virtual object for lens L2 which forms a final image I at distance PI=v. The ray diagram showing the image formation by the combination of these two thin convex lenses will be as shown below:
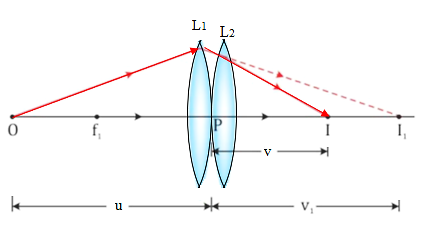
From the lens formula, for the image I1 formed by the lens L1, we can write it as
![]()
For the image formation by the second lens, L2:
![]()
Adding (1) and (2) we get:
![]()
![]()
If the two lenses are considered a single lens of focal length f, which forms an image I at a distance v with an object distance being u, then we get
![]()
![]()
Hence, the above relation is the focal length of the combined system.
(b) Given AQ = AR.
![]() ∠AQR = ∠ARQ.
∠AQR = ∠ARQ.
The ray diagram for the refraction of ray PQ passing through the prism ABC is as
shown below.
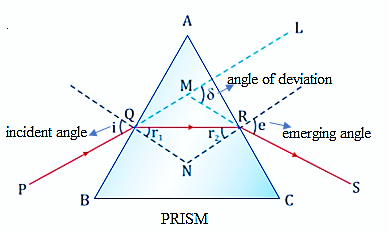
When the ray PQ emerges from face AC at point R of the prism after refraction from surface AB, it implies that the refracted ray QR travels parallel to the base of the prism. This happens at the minimum deviation position. So, according to the angle of minimum deviation formula, we have
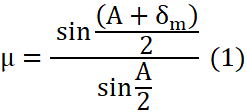
where A is the angle of prism, is ![]() the angle of minimum deviation and
the angle of minimum deviation and ![]() is the refractive index of the prism.
is the refractive index of the prism.
In the question, it is given that, A =![]() , n =
, n = ![]()
Substituting in (1) we get

On solving the above expression, we get
![]()
Thus, the angle of minimum deviation = 60°.
At the minimum deviation position, angle of incidence i will be
![]()
Substituting the given values, we get i=![]()