(i) In Young’s double slit experiment, deduce the condition for (a) constructive, and (b) destructive interference at a point on the screen. Draw a graph showing variation of intensity in the interference pattern against position ‘x’ on the screen.

(ii) Compare the interference pattern observed in Young’s double slit experiment with single slit diffraction pattern, pointing out three distinguishing features.

OR

(i) Plot a graph to show variation of the angle of deviation as a function of angle of incidence for light passing through a prism. Derive an expression for refractive index of the prism in terms of angle of minimum deviation and angle of prism.

(ii) What is dispersion of light? What is its cause?

(iii) A ray of light incident normally on one face of a right isosceles prism is totally reflected as shown in fig. What must be the minimum value of refractive index of glass? Give relevant calculations.

(i) Let us first explore the fringe width in Young’s Double slit experiment by drawing the double slit diagram.

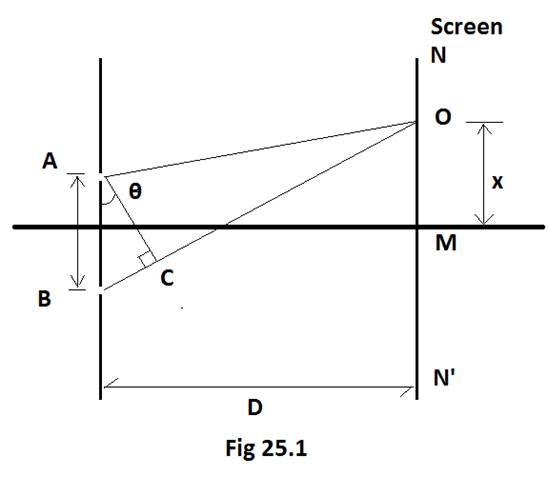
The slit are at a distance of “d” from each other, the distance on the screen at point O to M is “x” and the distance between the screen and the slits is “D”. Now the intensity is maximum, at point M due to path difference, which is zero.

Let us denote the path difference as P

Therefore, the path difference is P = BO – AO = BO – CO = BC

In the right angle triangle of ABC, P =

(a) For Constructive Interference

Now it is considered that the path difference is equivalent to the integral multiple of wavelength ().

where

n is the number of fringes, λ is the wavelength, x is the distance from the middle of the screen to point O, D is the distance between the slits and the screen.

(b) For Destructive Interference

As for destructive interference, the distance (x) is

The graph showing variation of intensity in the interference pattern,

against position ‘x’ on the screen.

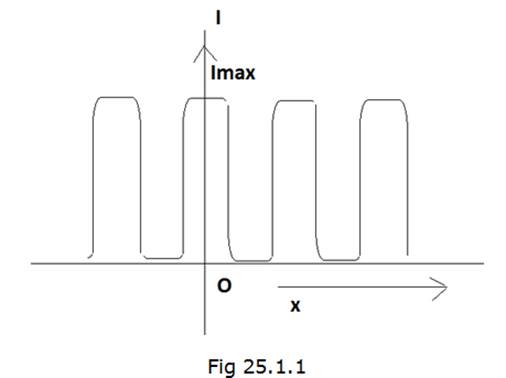
(ii) Comparing the interference pattern observed in Young’s double slit experiment with single slit diffraction pattern

1. The interference pattern have bright fringes with same intensity while vice versa is true for the diffraction pattern.

2. In interference pattern, the dark fringes have zero visibility while in diffraction pattern the dark fringes are easily prominent.

3. The widths of the fringes are same in single slit diffraction pattern as compared in interference pattern.

OR (i)

If the incidence angle is increased with time the deviation decreases to minimum deviation at a value of and then it increases again from the point of minimum deviation towards x-axis.

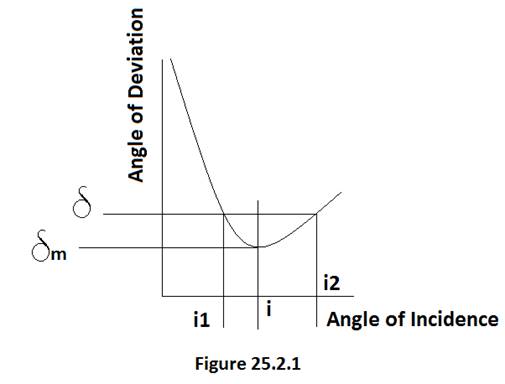
When the angle of deviation is at point “i” then

The refraction angles of the prism are

Now the refraction angle can be written in terms of angle of prism

If the angles of refraction are same then, the common angle of refraction is

Now finding the angle of incidence in term of prism angle is

Hence, the refractive index of the prism can be found out by the formula of Snell’s Law;

Therefore, the refractive index in terms of minimum deviation and angle of prism is

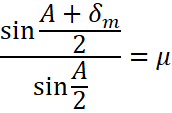
(ii)

The dispersion of the light is the splitting of the light ray into different colour mainly colour containing in the VIBGYOR. This dispersion happens because, the light beam carry wavelength of the different colour light, so when the light strikes the perfect angle it refracts into different colour at different position due to the change in wavelength.

(iii)

Let us see according to the diagram when the light ray falls on the point M of the surface AB it reflects out of the prism at from the surface CB. Therefore, the refractive index is calculated by

The angle C is the critical angle of the prism meaning the angle at which it will reflect perfectly at and out of the prism.

Let us take the angle C as, we have

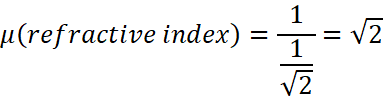
Therefore, the minimum value of the refractive index of the glass is 1.41