(i) Find the magnitude and direction of current in 1 V resistor in the given circuit.

(ii)Two student’s X and Y perform an experiment on potentiometer separately using the circuit diagram shown below.

Keeping other things unchanged (a) X increases the value of resistance R, (b) Y decrease the value of resistance S in the set up. How will these changes affect the position of null point in each case and why?

OR

(a) Use Kirchhoff’s rules, calculate the current in the arm AC of the given circuit.
(b) On what principle does the meter bridge work? Why are the metal strips used in the bridge?

(i) To solve the problem, we make use of Kirchhoff’s law.

From the figure,

——————(1)

And

——————(2)

Solving (1) and (2) we get

So the net current across 1Ω resistor is

The negative sign indicates that the direction is opposite to the assumed direction and hence from Q to P.

(ii)(a) In increasing the resistance R, the current flowing through AB decreases therefore, the potential difference across AB also decreases. To balance this potential, more wire is required. So, the null point sifts towards B.

(b) Following the same logic, as the resistance decreases, the current increases and hence the potential gradient increases and we require a shorter wire for balance conditions. Hence, the balance point shifts towards A.

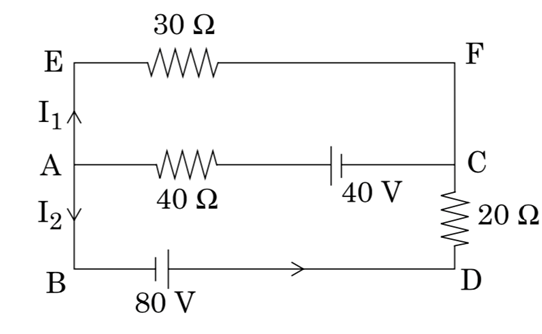
OR

(a) Here, we apply Kirchhoff’s rule in loop AEFC

—————(1)

Again in loop BEFD,

—————(2)

And, —————(3)

From eqn (1) and (3),

—————(4)

Solving eqn (2) and (4), we get,

and

using this in eqn (3)

(b) Meter bridge works on the same principle as the Wheatstone bridge. The resistances across the bridge are balanced to give a null condition where no current flows through the galvanometer.

Thick connections are used to connect wires as this minimizes the resistance of these connections. If this is not done, then we need to take into account the resistances due to connections.