Prove that the tangents at the extremities of any chord of a circle make equal angles with the chord.

Question

Philoid · Accepted Answer

Let the circle with centre O and chord PQ with tangents from point A as AP and AQ as shown:

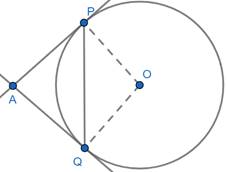
We have to prove that ∠APQ = ∠AQP

Consider ΔOPQ

⇒ OP = OQ …radius

Hence ΔOPQ is an isosceles triangle

⇒ ∠OPQ = ∠OQP …base angles of isosceles triangle …(a)

As radius OP is perpendicular to tangent AP at point of contact P

⇒ ∠APO = 90°

From figure ∠APO = ∠APQ + ∠OPQ

⇒ 90° = ∠APQ + ∠OPQ

⇒ ∠APQ = 90° - ∠OPQ …(i)

As radius OQ is perpendicular to tangent AQ at point of contact Q

⇒ ∠AQO = 90°

From figure ∠AQO = ∠APQ + ∠OPQ

⇒ 90° = ∠AQP + ∠OQP

⇒ ∠AQP = 90° - ∠OQP

Using (a)

⇒ ∠AQP = 90° - ∠OPQ …(ii)

Using (i) and (ii), we can say that

⇒ ∠APQ = ∠AQP

Hence proved

Hence, the tangents at the extremities of any chord of a circle make equal angles with the chord